• Printer Friendly Version
• Add to My ePortfolio

Subject

Math, Science & Technology

Learning Context/ Introduction

First-grade students are asked to work with a partner to solve a problem about buying pumpkins. The problem could be made easier or more difficult by changing the total amount of money the pumpkins cost, or by asking each pair or group of students to find as many solutions as possible.

Materials Needed

1. At least 4 pumpkins—1 large, 1 medium, and 2 small (if real pumpkins are not available, you could use paper cut-outs of pumpkins)
2. A variety of mathematic manipulatives and collections for the students to use to “stand for” the pumpkins as they work out their solution(s)
3. Paper (white & orange), pencils, crayons/markers
4. Large chart paper to record the brainstorming and the multiple solutions during the class discussion

Procedure

1. Present the following problem to the students: I went to the pumpkin farm with $5.00 to spend. Big pumpkins were $2.00. Medium pumpkins were $1.00. Small pumpkins were 2 for $1.00. I spent all of my money. What kind of pumpkins could I buy?
2. Place the pumpkins on a table with a sign showing the prices of each kind of pumpkin. Refer to them as you describe the problem.
3. Explain that students may use any materials in the room, or draw, to help them solve this problem. Brainstorm a list of mathematic manipulatives that they use to stand for the pumpkins as they work on solving this problem.
4. After students have solved the problem, they should write and/or draw to explain how they solved it. Give them an opportunity to share their solution(s) with the class.
5. The students then work in pairs or small groups. The teacher should circulate throughout the room to observe them and to conference where needed.
6. As students finish, they should share their solutions. The teacher should record the various solutions on chart paper so that they can see the multiple solutions and check to see if their solution has been mentioned.

Assessment

1. Observe and record student participation in class discussion by audio-taping and making written notes during and/or after the lesson regarding:
   • ability to explain reasoning
   • willingness to take risks
   • level of involvement and interest in the assignment
   • inventiveness in thinking about how to solve the problem.
2. Observe and record information about the student’s work with a partner by taking brief notes during the work session and talking to groups as they work through the problems regarding:
   • grasp of numerical relationships
   • ability to represent numerical relationships with words and symbols
   • process of working with others
   • choice of materials and how they were used to solve the problem
   • level of involvement in the process.
3. Review the written work done by the students, making notes on the information gained and using the process of analyzing the work to plan the next steps in the instructional process, in terms of individual students and of the class as a whole.

Student Work

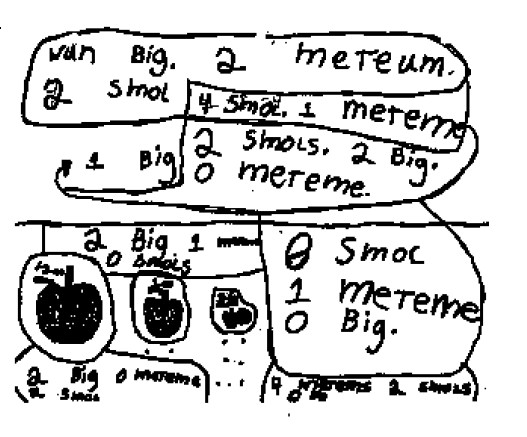
Author

Merri Jones Earl
John Harshaw Primary School
Chenango Forks Central School District
Binghamton, NY 13901

Source

Earl, Merri Jones "Harvest Halloween." Mathematics Resource Guide with Core Curriculum. New York State Education Department, 175-176.

Adapted from: Caren, Ann, Beverly J. Martin School, Ithaca City Schools.

Objectives

1. To solve a "real" problem that is connected to students’ interests (and is integrated with other curriculum areas, i.e., science, social studies, health).
2. To relate mathematics to things students do outside of school (with their families) and thus to see that mathematics is present and useful (both inside and outside the classroom).
3. To see that a problem can have more than one solution.
4. To develop students’ ability to communicate mathematically through writing and/or drawing and to share their thinking (with others) through class discussion.
5. To foster curiosity about mathematics and to make connections between mathematics and other subject areas.

Related Academic Standards

New York State

NY-1.OA.1 Use addition and subtraction within 20 to solve one step word problems involving situations of adding to, taking from, putting together, taking apart, and/or comparing, with unknowns in all positions.

NY-1.OA.2 Solve word problems that call for addition of three whole numbers whose sum is less than or equal to 20.

NY-1.OA.6a Add and subtract within 20. Use strategies such as:

• counting on;
• making ten;
• decomposing a number leading to a ten;
• using the relationship between addition and subtraction; and
• creating equivalent but easier or known sums.

NY-1.OA.6b Fluently add and subtract within 10.

1.OA.1 Use addition and subtraction within 20 to solve word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using objects, drawings, and equations with a symbol for the unknown number to represent the problem.

View All