Hello, Guest!

Lesson Plan

Investigation - Symmetry


Subject

Math, Science & Technology

Grade Levels

Intermediate, 5th Grade


Vocabulary

Symmetry, rotational, congruent, horizontal, vertical

Authors

The Core Curriculum Companion For The New York State Mathematics Resource Guide Writing Team.

Duration

2-3 lessons

Procedure

DOING THE INVESTIGATION

  1. Give each pair of students two of the pattern block shapes, graph paper, rulers, crayons, and scissors.
  2. Display the square and ask the students how we could determine whether it has a line of symmetry using the material we have. (We could trace it onto graph paper and use the ruler to draw a line that we think will be a line of symmetry. Cut the figure out and fold it on the line to see if the 2 parts fit exactly on one another.)
  3. Have the students discuss a strategy for finding out if the square has rotational symmetry. (We could trace the square, cut it out and lay it on top of the pattern block square. Rotate it around a point at the center until a different vertex is at the top. If it fits exactly, i.e. is congruent, when a different vertex is at the top, it has rotational symmetry.)
  4. Have each pair of students work together to determine whether the two pattern block shapes they were given have line symmetry and/or rotational symmetry. If a shape has line symmetry, the students should find out how many lines of symmetry it has.
  5. Have students share the results of their investigations. They should examine each other's drawings and discuss generalizations about lines of symmetry.

POSSIBLE SOLUTIONS


Generalizations may include: Equilateral triangles have 3 congruent sides and angles and 3 lines of symmetry; squares have 4 congruent sides and angles and 4 lines of symmetry, etc.

Extending The Activity


  1. Give each student a set of the 6 different pattern blocks, graph paper, crayons, and a ruler.
  2. Have the students draw a vertical line down the center of the graph paper. This will be a line of symmetry. On one side of the line, each student will use the pattern blocks to create a geometric design and color it.
  3. Collect all the designs and place them in a large box. Have each student select a design from the box (not his/her own) and create the symmetrical design on the other side of the line.
  4. The designs may be taped together to form a large .quilt. of symmetrical designs that can be displayed in the room.

Description

For each pattern block shape, determine whether it has line symmetry, rotational symmetry, or both kinds of symmetry. If the figure has line symmetry, determine how many lines of symmetry it has.

WHAT'S THE MATHEMATICS?

  • recognize and demonstrate line symmetry
  • recognize and demonstrate rotational symmetry
  • recognize and name geometric figures
  • understand congruence
  • solve problems

Assessment 1

How many of the letters below have both a horizontal and a vertical line of symmetry?

A E I O U

a) 5
b) 4
c) 3
d) 2

Ans. d

Assessment 2

a. Examine the isosceles triangle and the pentagon below. Draw as many lines of symmetry as you can for each.


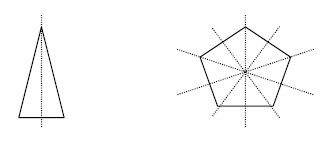
(Lines of symmetry shown as dashed lines indicate answers.)

b. Predict which of the above shapes will also have rotational symmetry. (the pentagon)

c. Explain why you believe your prediction is correct.

(Accept reasonable answers, e.g., the pentagon has more than one line of symmetry so I predict it will also have rotational symmetry OR the pentagon has 5 congruent sides and angles so I predict it will have rotational symmetry.

Additional Notes

For additional information and activities, see pages 70, 71, 82, and 83 in the New York State Core Curriculum/Mathematics Resource Guide.

  • About The Core Curriculum Companion

    • Source

    The Core Curriculum Companion For The New York State Mathematics Resource Guide Writing Team. "Symmetry". In The Core Curriculum Companion For The New York State Mathematics Resource Guide, 143-146.

    Related New York City Performance Standards

    • M2a Is familiar with assorted two- and three-dimensional objects, including squares, triangles, other polygons, circles, cubes, rectangular prisms, pyramids, spheres, and cylinders.
    • M2e Recognizes similarity and rotational and bilateral symmetry in two- and three- dimensional figures.
    • M2k Models situations geometrically to formulate and solve problems.
    • M5a Formulation
    • M5b Implementation
    • M5c Conclusion
    • M5d Demonstrates mathematical reasoning by generalizing patterns, making conjectures and explaining why they seem true, and by making sensible, justifiable statements.
    • M6e Refers to geometric shapes and terms correctly.


    Data is Loading...
    .
    .