Lesson Plan

Investigation - Looking For Triangles
Subject
Math, Science & Technology
Grade Levels
Intermediate, 7th Grade
Materials
Pattern blocks
Authors
The Core Curriculum Companion For The New York State Mathematics Resource Guide Writing Team.
Extending The Activity
Have them create a similar growing design 1, 2 and 3 using their hexagons.
Part A: If the pattern continues, how many small hexagons must be added to
the 17th design to make the next design. Show your work.
Part B: Give a general rule. Explain.
Assessment 1
In the growing design using triangles the number of triangles varies directly
as the design number. What would be the graph of this generalization?
| a. a straight line |
| b. a parabola |
| c. the positive side of the parabola |
| d. an "s" curve |
Ans. c (Since we are only concerned with positive numbers.)
Assessment 2
If the difference in the number of triangles between two designs in the investigation
is 23, what are the two design numbers? Explain.
Ans. The design numbers are 11 and 12. One strategy to use is to work backwards
from the generalization D = 2F + 1, solve for F where D = 23.
Additional Notes
For additional information and activities, see pages 111 and 116 in the New York State Core Curriculum/Mathematics Resource Guide.
About The Core Curriculum Companion
Source
The Core Curriculum Companion For The New York State Mathematics Resource Guide Writing Team. "Looking For Triangles". In The Core Curriculum Companion For The New York State Mathematics Resource Guide, 200-203.
Related New York City Performance Standards
- M3a Discovering, describing, and generalizing patterns, including linear,
exponential and simple quadratic relationships.
- M3b Representing relationships with tables, graphs in the coordinate plane,
and verbal or symbolic rules.
- M3c Analyzing tables, graphs, and rules to determine functional relationships.
- M5a Formulation
- M5b Implementation
- M5c Conclusion
Duration
1 lesson
Procedure
DOING THE INVESTIGATION
- Discuss with your students the meaning of the word pattern.
- Have your students suggest some patterns, e.g. number patterns, geometric patterns and other patterns
- Guide your students to look at growing patterns.
- Have your students create their own growing patterns with the pattern blocks.
- You may draw these designs or have your students use pattern blocks. Have your students examine the following designs (patterns):
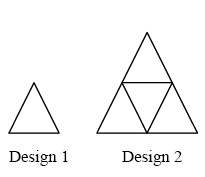

- Pose the problem, "If the above pattern continues, how many small triangles must be added to design 17 to make design 18. Show your work."
- Using the information they have, ask your students to work in groups to give a general rule which will find the number of small triangles that are needed in any design number.
POSSIBLE SOLUTIONS
The answer is 35. One strategy is to keep drawing triangles. Another is to create a chart and look for patterns that will help.
| Design (F) |
Total Number of Triangles (T) |
Difference From this Design to the Next (D) |
| 1 |
1 |
3 |
| 2 |
4 |
5 |
| 3 |
9 |
7 |
| 4 |
16 |
9 |
| 5 |
25 |
11 |
| 6 |
36 |
13 |
Notice the differences from any design to the next design is D=2F + 1 where D is the difference, F is the figure number of the current shape and T the total number of triangles. Therefore, the difference between the 17th design and the 18th design is 2*17 + 1 = 35.
To find the number of triangles needed in any design, look at the chart. Notice that the total number of triangles is the design number squared: T= F squared. Squaring design 17 (289) and design 18 (324) is another way of determining the number of triangles that need to be added (324 - 289).
Vocabulary
Pattern, generalization
Description
Students will investigate a series of triangles, looking for patterns and generalizing what
they have found.
WHAT'S THE MATHEMATICS?
- identifying, describing, representing, extending, and creating patterns
- describing functions and generalizing by the use of rules and algebraic
expressions
- describing and representing numerical and geometric patterns and functions
using equations, graphs, and tables
- organizing and analyzing data resulting in function applications through
use of a table of values, sentence, formula, graph, and prediction
- examining a situation and determining if the quantities vary directly or
indirectly, and representing that variation graphically, in a table and in
an equation
- identifying the input and the output in a relationship between two variables
and determining whether the relationship is a function
- using patterns and functions to solve problems
